Bionetta

Introducing Bionetta — a blockchain-friendly, client-side zero-knowledge (ZK) proving framework for machine learning inference. Unlike existing ZKML solutions, Bionetta is designed to generate compact and efficient R1CS circuits optimized for Groth16-style proving and verification. This architecture enables exceptional performance on moderately sized models: proof sizes are just 160 bytes, verification requires only a few hash operations and four pairings, and proving a model with 1 million parameters takes under 20 seconds.

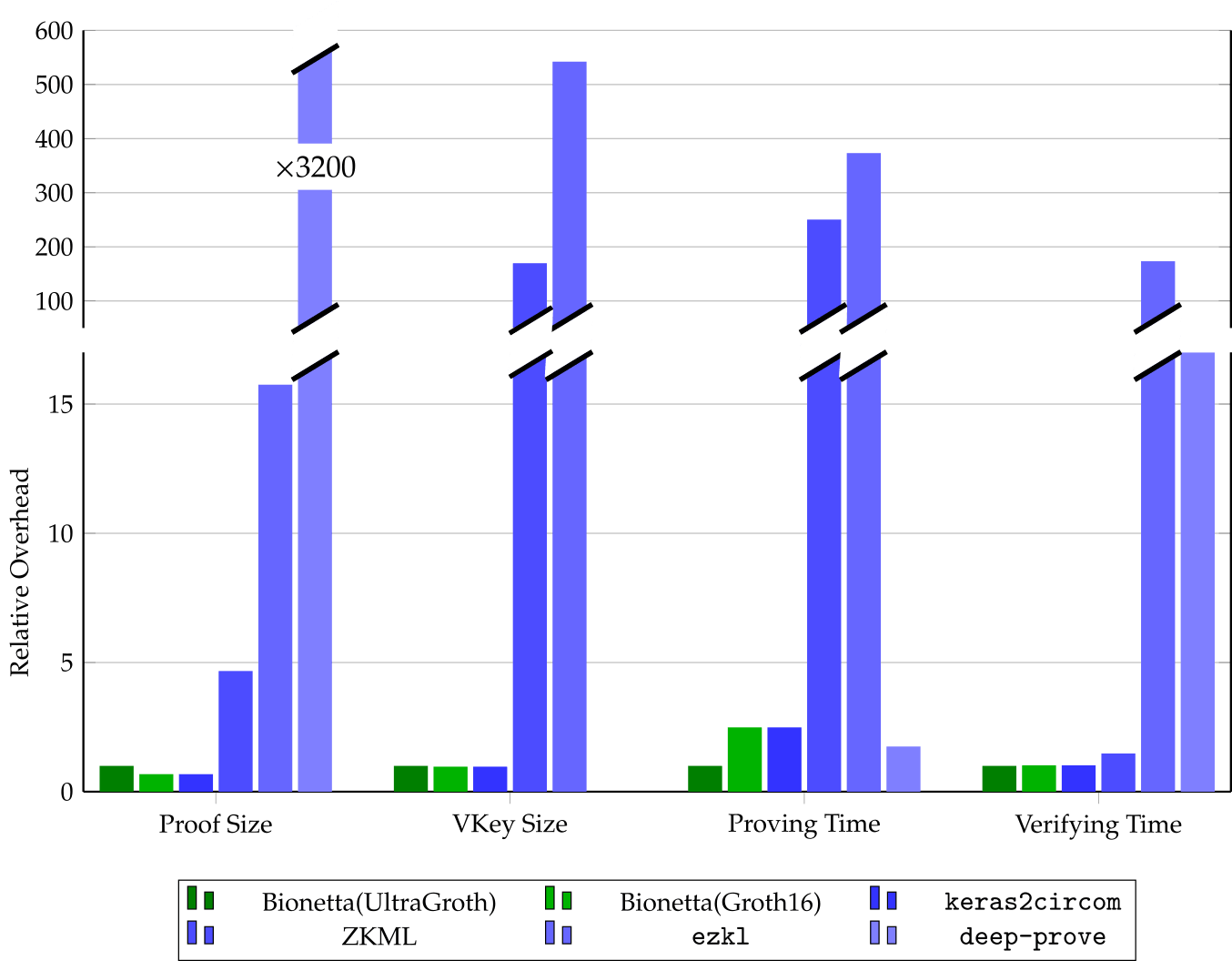
We evaluated our custom protocol against leading state-of-the-art frameworks, including EZKL, ddkang/zkml, keras2circom, and Lagrange’s deep-prove. Our benchmarks demonstrate that our solution significantly outperforms existing tools in both proving and verification efficiency—achieving over 3200× speedup compared to deep-prove, for example—while maintaining some of the fastest proving times in the field.

We fully embrace the concept of client-side proof generation. A key innovation in our approach is embedding model weights directly into the circuit, effectively eliminating the need to represent linear operations as constraints — since they require no cost during R1CS compilation. For example, in the case of linear regression, our method enables zero-constraint ZK proofs.

circuit LinearRegression(n: int):
- ≫ public signal input θ[n+1];
  private signal input x[n];
  public signal output y;
  y <== 0;

  # Scalar product (θ,x)
  for i in 1..n:
    y += θ[i] * x[i];

  # Adding the bias θ₀
  y <== y + θ[0];

+ const θ[n+1] = [0x642, 0x123, ...];
circuit LinearRegression(n: int):
  private signal input x[n];
  public signal output y;
  y <== 0;

  # Scalar product (θ,x): now costs 0
  for i in 1..=n:
    y += θ[i] * x[i];

  # Adding the bias θ₀
  y <== y + θ[0];

To streamline the workflow, Bionetta allows you to define neural networks using familiar tools such as TensorFlow or PyTorch, using supported layer types. Once defined, the model is passed to the Bionetta framework — which handles the rest, automatically generating the R1CS specification and producing all necessary bindings for proving and verification. Although the initial compilation may take some time, proof generation thereafter takes just seconds for the end-user.

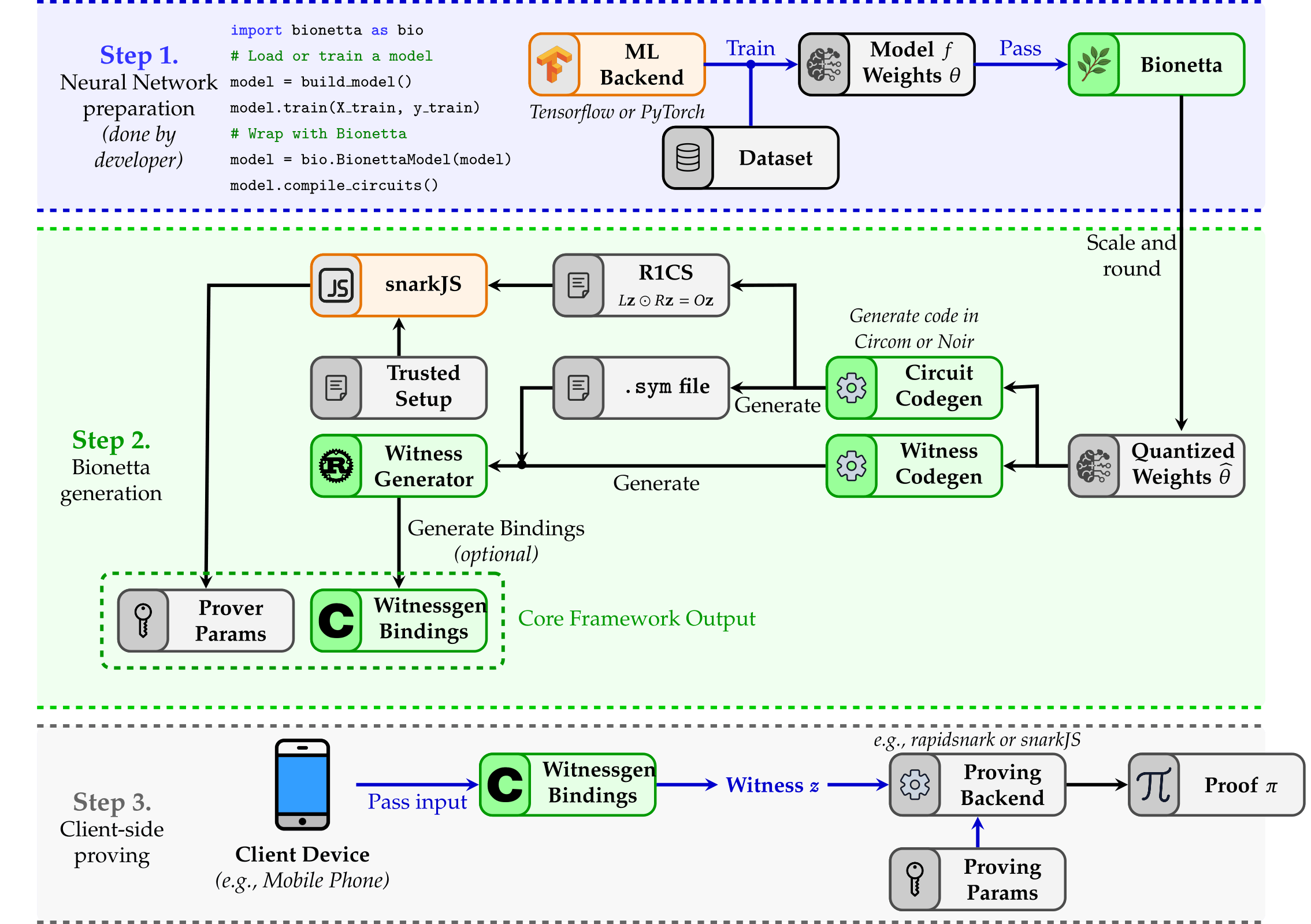
Bionetta is agnostic to the underlying ZK proving system, provided it supports R1CS. This flexibility allows integration with various backends such as Spartan, Hyrax, Aurora, or Fractal. Additionally, we introduce UltraGroth — an enhanced Groth16-based protocol that enables efficient use of lookup tables, reducing the average cost of non-linearity checks by up to 20×.

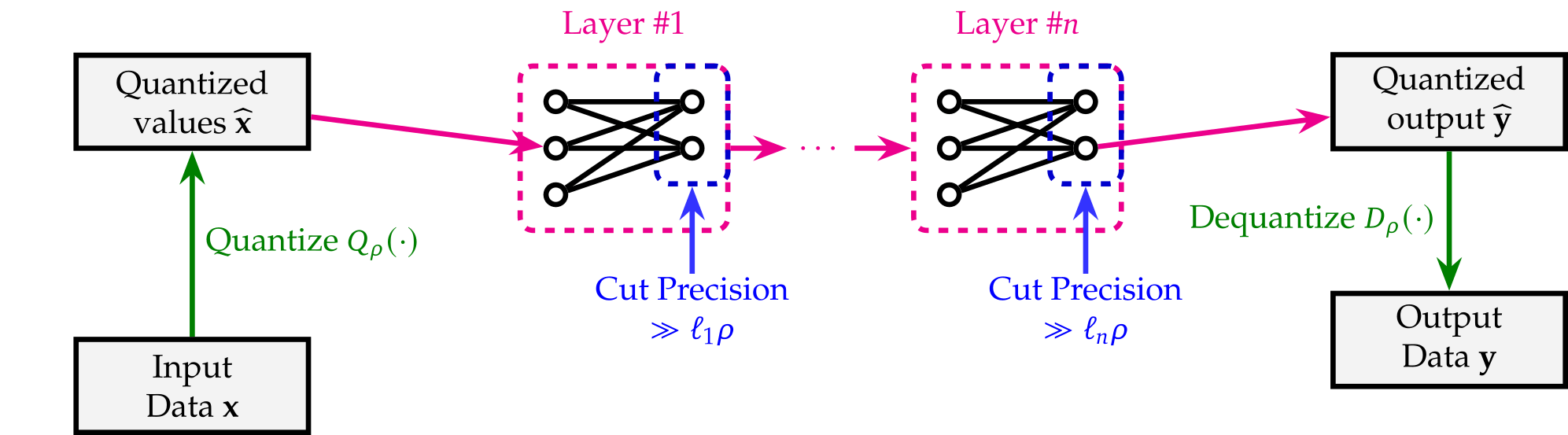
We utilize an efficient arithmetization strategy that introduces zero additional constraints when implemented in R1CS. This quantization approach effectively prevents neural network overflows—an issue observed in some frameworks like keras2circom—without requiring non-native arithmetic within the circuit.

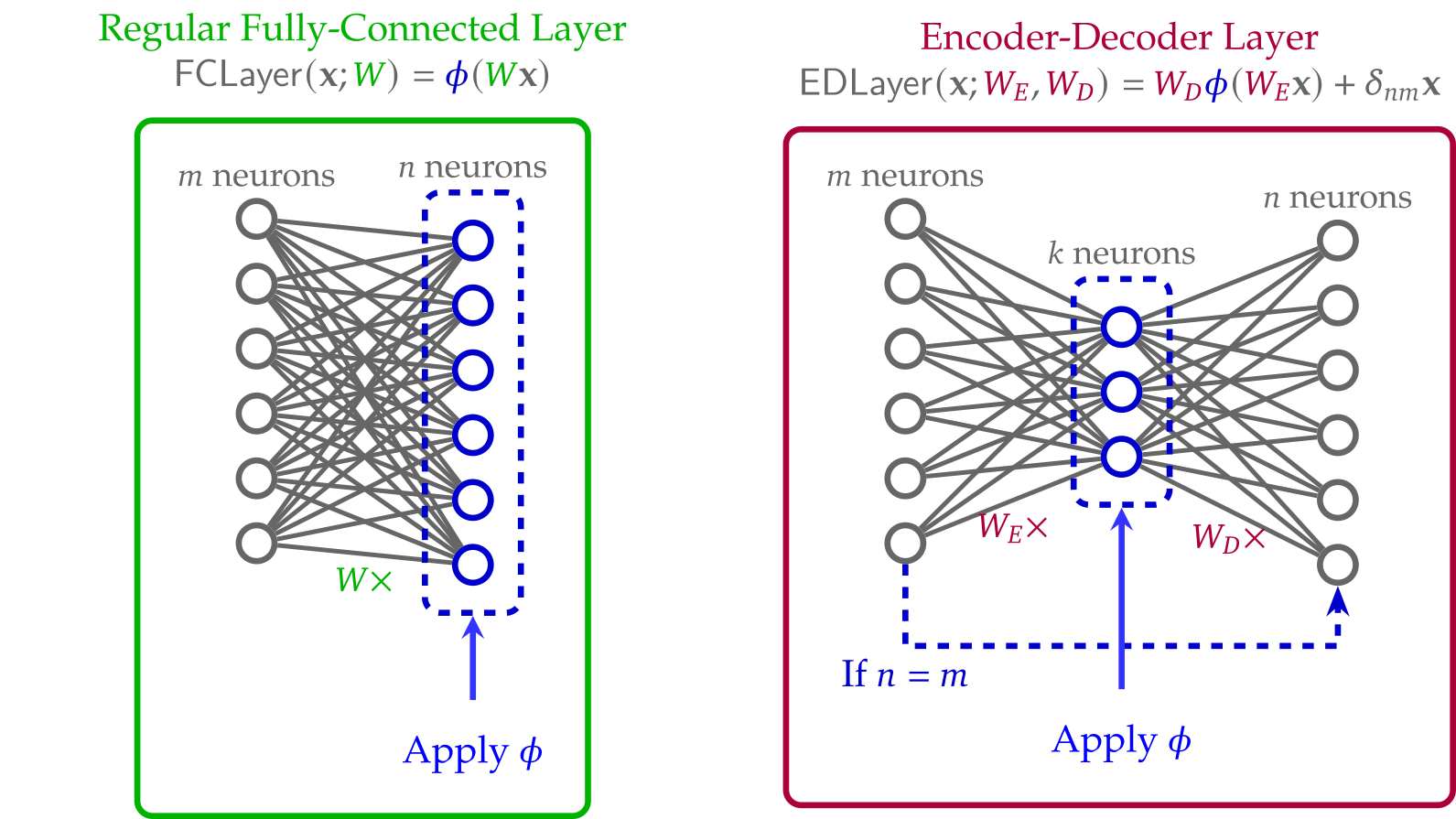
Finally, we propose a design approach for zero-knowledge-friendly neural network architectures that can be implemented more naturally and efficiently within R1CS circuits.